El mito de los nodos completos, S. Tominaga, también conocido como CSW

The Myth of Full Nodes
El mito de los nodos completos
S. Tominaga, también conocido como CSW
8 de octubre de 2024
https://x.com/CsTominaga/status/1843529362341277972?t=sj_pGpCHtWYuzNw62pPvYA&s=19
https://t.me/S_Tominaga/1133
Machine Translated by Google
Un análisis matemático de la conectividad en Bitcoin
Para comprender el verdadero papel de los nodos completos en la red de Bitcoin es necesario realizar un examen exhaustivo utilizando la teoría de grafos. Este análisis profundiza en los fundamentos matemáticos de la estructura de la red y explora por qué los nodos completos no ayudan significativamente en la propagación de transacciones y, de hecho, introducen ineficiencias. Al centrarnos en la topología de la red, las diferencias de latencia y los principios de la teoría de grafos, podemos demostrar rigurosamente la naturaleza superflua de los nodos completos y su impacto mínimo en la funcionalidad de la red.
Descripción general de la topología de la red de Bitcoin
La red de Bitcoin se puede visualizar como una combinación de dos subredes distintas:
– Nodos de minería (pools): una red estrechamente interconectada de 13 a 15 nodos de minería, que son esencialmente pools de minería. Estos forman un gráfico completo, donde cada nodo de minería está conectado directamente con todos los demás.
– Nodos completos: entre 5000 y 10 000 nodos completos con un promedio de 8 conexiones cada uno, formando una red dispersa con patrones de conectividad aleatorios.
Esta diferencia en la topología es fundamental para comprender cómo se propagan las transacciones a través de la red y por qué a menudo se exagera el papel de los nodos completos.
Nodos de minería: una estructura de gráfico completa
En la teoría de grafos, un grafo completo KnK_nKn se define como un grafo donde cada uno de los nnn nodos está conectado directamente con todos los demás nodos. Para la red de pools de minería de Bitcoin, sea n=15:
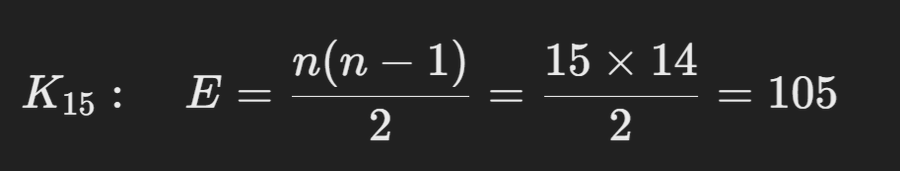
Esto significa que hay 105 bordes directos entre los 15 nodos de minería. Cada borde representa una conexión de baja latencia, con una latencia de entre 5 ms y 15 ms por conexión. Esta estructura completamente conectada permite que cualquier información (por ejemplo, una transacción) llegue a todos los demás nodos en un solo paso.
Diámetro del gráfico: en un gráfico completo, el diámetro (la ruta más larga y más corta entre dos nodos) es 1. Esto significa que la distancia entre dos nodos es un solo borde, lo que hace que la propagación de la información sea extremadamente eficiente. El diámetro D de K_{15} es:.
D = 1
Tiempo de propagación: dado el rango de latencia de 5 ms a 15 ms, el peor tiempo para que una transacción se propague por toda la red de nodos de minería es:
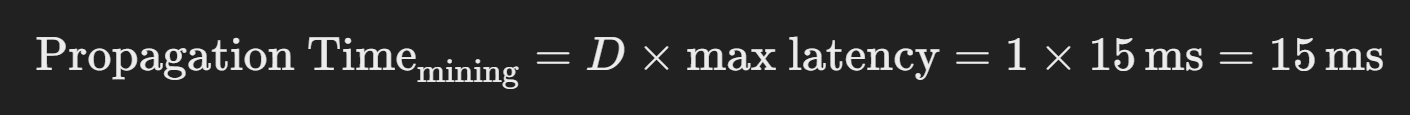
Este es un escenario ideal para una red de mundo pequeño, donde todos los nodos pueden compartir información de inmediato, lo que garantiza una rápida difusión de las transacciones.
Nodos completos: estructura de gráfico aleatorio
Los nodos completos, por el contrario, forman un gráfico aleatorio, que es mucho menos eficiente en términos de conectividad y velocidad de propagación. Analicemos esta estructura con más detalle:
Representación de gráfico aleatorio: un gráfico aleatorio G(n, p) se define mediante n nodos, cada uno conectado con una probabilidad p. Para la red de nodos completa de Bitcoin, n = 5000 y el grado promedio k = 8:
p = k / (n – 1) = 8 / 4999 ≈ 0,0016
La probabilidad de que dos nodos cualesquiera estén conectados es extremadamente baja en comparación con la red minera. Esto da como resultado un gráfico escasamente conectado, con muchos nodos más separados en términos de saltos.
Longitud de ruta promedio: La longitud de ruta promedio L en un gráfico aleatorio se puede estimar utilizando:
L ≈ log(N) / log(k)
Sustituyendo N = 5000 y k = 8:
L ≈ log(5000) / log(8) ≈ 3,7 / 0,9 ≈ 4,1
Esto significa que, en promedio, una transacción tarda alrededor de 4 saltos en viajar entre dos nodos completos en esta red aleatoria.
Diámetro del gráfico: El diámetro D de un gráfico aleatorio con 5000 nodos y un grado promedio de 8 se puede estimar como:
D ≈ 2 × log(N) / log(k) ≈ 2 × 4,1 ≈ 8,2
Por lo tanto, la ruta más corta más larga entre dos nodos completos puede ser de hasta 8 saltos.
Para calcular la cantidad promedio de conexiones necesarias para que una transacción viaje desde un nodo completo que se conecta inicialmente a la red y llegue a todos los nodos mineros, debemos considerar lo siguiente:
1- Hay aproximadamente 5000 nodos completos. Cada nodo completo tiene un promedio de 8 conexiones.
2- Hay entre 13 y 15 nodos mineros, que forman un gráfico completo. En un gráfico completo, cada nodo minero está conectado directamente a todos los demás nodos mineros.
3- Se da por sentado que existe una probabilidad del 99 % de que cualquier nodo completo esté conectado al menos a un nodo minero a través de una de sus 8 conexiones.
Paso 1: Probabilidad y conexiones iniciales
Dado que existe una probabilidad del 99 % (p_m = 0,99) de que un nodo completo se conecte a un nodo minero, la probabilidad restante de que un nodo completo no esté conectado directamente a ningún nodo minero es 1 – p_m = 0,01.
Paso 2: Número promedio de saltos
Dado que el 99 % de los nodos completos están conectados directamente a al menos un nodo minero, la mayoría de las transacciones llegarán a un nodo minero en solo 1 salto.
Para el 1 % de los casos en los que un nodo completo no está conectado directamente a un nodo minero, la transacción primero debe pasar por otros nodos completos antes de llegar a un nodo minero.
La longitud de ruta promedio en un gráfico aleatorio con 5000 nodos y un promedio de 8 conexiones es aproximadamente:
L = log(5000) / log(8) = 3,7 / 0,9 = 4,1 saltos.
Por lo tanto, en este 1 % En este escenario, la transacción requiere aproximadamente 4,1 saltos para llegar a un nodo completo que está conectado a un nodo minero y, luego, un salto adicional para llegar a la red minera, lo que hace un total de 5,1 saltos.
Paso 3: Promedio de saltos esperados
Para encontrar la cantidad total esperada de saltos para que una transacción llegue a un nodo minero, calculamos el promedio ponderado en función de las probabilidades:
E(saltos) = (0,99 * 1) + (0,01 * 5,1) E(saltos) = 0,99 + 0,051 E(saltos) = 1,041
Esto significa que, en promedio, se necesitan aproximadamente 1,041 saltos para que una transacción que comienza en un nodo completo llegue a un nodo minero. Este resultado está dominado por la alta probabilidad (99%) de que un nodo completo esté conectado directamente a un nodo minero, lo que hace que el número promedio de saltos sea muy cercano a 1.
Paso 4: Propagación a todos los nodos mineros
Una vez que una transacción llega a cualquier nodo minero, se propaga inmediatamente a todos los demás nodos mineros debido a la estructura gráfica completa de la red minera. Esto significa que el tiempo de propagación a través de la red minera es mínimo, ya que cada nodo minero se comunica directamente con todos los demás nodos mineros.
El número promedio de saltos para que una transacción desde un nodo completo llegue a la red minera es de aproximadamente 1.041. Dado que la mayoría de los nodos completos (99%) están conectados directamente a al menos un nodo minero, las transacciones generalmente llegan a la red minera casi de inmediato. La contribución del 1% restante de los casos en los que se necesitan más saltos es insignificante. Por lo tanto, el papel de los nodos completos en el proceso general de propagación de transacciones sigue siendo limitado, ya que los nodos mineros manejan la mayor parte de la difusión de transacciones de manera eficiente. Escenario: Desaparecen todos los nodos completos
Si desaparecen todos los nodos completos de la red de Bitcoin, nos quedan solo los nodos mineros. La red estará formada únicamente por los 13 a 15 nodos mineros, que forman un gráfico completo. En un gráfico completo, cada nodo (en este caso, cada nodo minero) está conectado directamente a todos los demás nodos mineros.
Eficiencia de la red sin nodos completos
1. Conectividad
Sin nodos completos, la red de Bitcoin se vuelve más pequeña pero más densa en términos de interconectividad. Los nodos mineros ya están completamente conectados, lo que significa que cada nodo minero se comunica directamente con todos los demás nodos mineros. Dado que las transacciones se propagan casi instantáneamente entre los nodos mineros, la eliminación de los nodos completos no interrumpirá esta comunicación directa.
– Con nodos completos: las transacciones de un nodo completo tardan más en llegar a los nodos mineros debido a los múltiples saltos en el gráfico disperso y aleatorio de nodos completos.
– Sin nodos completos: cada transacción se originaría o se transmitiría solo a través de los nodos mineros, lo que permitiría una propagación directa e inmediata entre ellos. Esto reduce los retrasos innecesarios causados por los nodos llenos.
2. Velocidad de propagación
– Con nodos completos: cuando una transacción se origina en un nodo completo, primero debe atravesar la red dispersa de nodos completos para llegar a un nodo minero. Esto agrega latencia al proceso, con un promedio de 1.041 saltos para que una transacción llegue a la red minera.
– Sin nodos completos: todas las transacciones se originarían en nodos mineros o se propagarían directamente dentro de la red minera. Dado que los nodos mineros están completamente conectados, el tiempo de propagación de la transacción sería mínimo, limitado solo por la velocidad de comunicación directa entre los nodos mineros, que es mucho más rápida que la red de nodos completos.
3. Impacto en la eficiencia de la red
– Eficiencia con nodos completos: los nodos completos contribuyen a cierta redundancia de la red, pero ralentizan la propagación de las transacciones debido a la naturaleza aleatoria y menos conectada de su estructura gráfica. Sus rutas más lentas agregan latencia innecesaria a la red.
– Eficiencia sin nodos completos: la red sería más eficiente sin nodos completos. Los nodos mineros, al estar estrechamente interconectados, manejan la propagación de transacciones de manera directa y rápida. Eliminar los nodos completos agilizaría el flujo de transacciones, reduciendo la latencia y haciendo que la red sea más rápida en general.
Conclusión
Si todos los nodos completos desaparecieran, la red de Bitcoin se volvería más eficiente. El gráfico completo de nodos mineros aún garantizaría una conectividad completa y una propagación rápida de transacciones. Los nodos completos agregan un valor mínimo al proceso de propagación y, de hecho, introducen ineficiencias debido a sus conexiones más lentas y de múltiples saltos. Por lo tanto, sin nodos completos, la red operaría con menor latencia y mejor rendimiento.
Implicaciones de la teoría de grafos: por qué los nodos completos son ineficientes
Las diferencias en la estructura del grafo y la latencia revelan fallas fundamentales en la suposición de que los nodos completos son críticos para la propagación de transacciones de Bitcoin:
1- Conectividad redundante: los nodos completos no agregan rutas útiles para las transacciones. En cambio, introducen rutas redundantes que son más lentas y, en última instancia, se ignoran una vez que los nodos mineros han completado su propagación.
2- Eficiencia de mundo pequeño: la estructura de mundo pequeño de la red minera, con un diámetro de 1, le permite compartir información de manera mucho más eficiente que las conexiones extensas y de alta latencia de los nodos completos. Esto garantiza que las transacciones siempre se procesan a través de la ruta más rápida, entre nodos mineros.
3- Falta de influencia en el control de la red: desde una perspectiva de descentralización, solo los nodos involucrados en la minería influyen en qué transacciones se incluyen en los bloques. Los nodos completos, al simplemente observar y transmitir, no participan en la toma de decisiones o la creación de bloques, lo que los hace irrelevantes para el concepto central de descentralización.
Los nodos completos agregan complejidad sin beneficio
Este análisis detallado basado en la teoría de grafos demuestra que los nodos completos son, en el mejor de los casos, una presencia pasiva en la red de Bitcoin. La eficiencia de la propagación de transacciones está impulsada completamente por los nodos mineros estrechamente conectados, que pueden difundir transacciones a través de la red en menos de 15 ms. La adición de miles de nodos completos, cada uno con mayor latencia y longitudes de ruta más largas, no mejora este proceso; en cambio, lo ralentiza.
La conclusión principal es que los nodos completos, que no participan en la minería, agregan poco valor al funcionamiento de Bitcoin. Sus velocidades de propagación más lentas y los esfuerzos redundantes para transmitir transacciones los hacen superfluos. La verdadera eficiencia y seguridad de la red reside en sus nodos mineros, que son los únicos que controlan los procesos críticos de inclusión de transacciones y creación de bloques.
En resumen, la creencia de que los nodos completos contribuyen a la descentralización o la eficiencia de la red es una interpretación errónea del diseño de Bitcoin. La descentralización en Bitcoin solo tiene sentido cuando se relaciona con la minería, no con un conjunto de observadores pasivos. El enfoque debe permanecer en la estructura efectiva y de baja latencia de la red minera, ya que esto es lo que sustenta la integridad y velocidad operativas de Bitcoin.
Un análisis riguroso de la teoría de grafos de la red de Bitcoin: la redundancia de los nodos completos con el flujo de transacciones probabilístico
Para demostrar aún más la redundancia de los nodos completos en la propagación de transacciones de Bitcoin, debemos ampliar nuestro análisis para incluir la probabilidad de que los nodos, como Alice y Bob, se conecten a la red del grupo de minería. Este análisis integrará modelos probabilísticos para evaluar la probabilidad de conexiones y su impacto en la velocidad y la ruta de las transacciones entre Alice y Bob, lo que resalta aún más la ineficiencia de los nodos completos. Descripción general de la estructura y la conectividad de la red
La red de Bitcoin se puede dividir en dos capas principales:
– Nodos de minería (pools): un conjunto altamente interconectado de 13 a 15 nodos de minería que forman un gráfico completo K_n, donde cada nodo está conectado directamente a todos los demás, lo que facilita el intercambio rápido de información.
– Nodos completos: una red más amplia pero más dispersa de aproximadamente 5000 a 10 000 nodos completos, cada uno de los cuales mantiene un promedio de 8 conexiones. Estos nodos generalmente se conectan aleatoriamente a otros nodos completos o directamente a uno o más nodos de minería.
Este análisis incorporará ahora las probabilidades de conexión entre nodos como Alice y Bob y los nodos de la red (pools de minería), lo que ilustra el efecto de estas probabilidades en la propagación de transacciones.
Probabilidad de conexión a nodos de minería
Sea p_m la probabilidad de que un nodo completo determinado (como Alice o Bob) esté conectado directamente a al menos un nodo de pool de minería. Dados los patrones de conectividad en la red de Bitcoin, es razonable suponer que una proporción significativa de nodos completos están conectados a nodos de minería. Sin embargo, el valor exacto de p_m puede verse influenciado por las configuraciones de red y las preferencias de los nodos individuales.
Para este análisis, supongamos:
– p_m = 0,99: una alta probabilidad de que cualquier nodo completo dado, como Alice o Bob, esté conectado al menos a un nodo de grupo de minería, lo que refleja la realidad de que la mayoría de los nodos completos se conectan a nodos de minería para un mejor acceso a los datos de la red.
– p_f = 0,01: la probabilidad restante de que un nodo completo esté conectado solo a otros nodos completos, sin ninguna conexión directa a los nodos de minería.
Análisis probabilístico del flujo de transacciones entre Alice y Bob
Ahora, considere el flujo de transacciones entre Alice y Bob en diferentes escenarios:
Escenario 1: Conexión directa a un nodo de minería: si Alice está conectada directamente a un nodo de minería, la probabilidad de que su transacción llegue a la red de minería inmediatamente es p_m. Lo mismo se aplica a Bob con probabilidad p_m. La probabilidad de que tanto Alice como Bob estén conectados directamente a la red de minería es:
– P_direct = p_m * p_m = 0,99 * 0,99 = 0,9801
– Esto significa que hay un 98,01 % de posibilidades de que tanto Alice como Bob estén conectados a al menos un nodo minero. En este caso, la transacción de Alice, al ser enviada, llega rápidamente al nodo minero y se propaga a través de toda la red minera en cuestión de milisegundos. Una vez que la transacción se propaga por completo entre los nodos mineros, llegará a Bob a través de su conexión a la red minera. El tiempo que tarda la transacción en llegar a todos los nodos mineros es aproximadamente:
Tiempo de propagación_minería = 15 ms
Bob, al estar conectado directamente a la red minera, recibe la transacción casi tan pronto como los nodos mineros la han propagado, lo que resulta en una transmisión muy eficiente.
Flujo de transacción.
Escenario 2: Conexión indirecta a través de nodos completos: si Alice o Bob forman parte del 1 % de nodos que no están conectados directamente a ningún nodo minero (p_f), deben confiar en sus conexiones a otros nodos completos para propagar la transacción. La probabilidad combinada de que ni Alice ni Bob estén conectados directamente a un nodo minero es:
– P_indirect = p_f * p_f = 0,01 * 0,01 = 0,0001
Esto significa que hay una probabilidad del 0,01 % de que tanto Alice como Bob carezcan de una conexión directa a un nodo minero. En este escenario poco común, la propagación de la transacción tendría que ocurrir a través de las rutas más lentas y de múltiples saltos de la red de nodos completos: Impacto en la latencia del nodo completo: una transacción de Alice viajaría a través de aproximadamente 4 saltos en la red aleatoria de nodos completos antes de llegar potencialmente a un nodo minero, y cada salto demoraría entre 60 y 80 ms. El tiempo total de propagación antes de llegar a un nodo minero sería:Tiempo de propagación_nodos completos = 4 * 70 ms = 280 ms Una vez que la transacción llega a un nodo minero, se propaga rápidamente a través de la red minera. Sin embargo, debido al retraso inicial a través de la red de nodos completos, la transacción llega a Bob mucho más tarde de lo que hubiera llegado si Alice hubiera tenido una conexión directa a la red minera.
Impacto de la redundancia: rechazo de transacciones duplicadas
Dada la alta probabilidad (p_m = 0,99) de que Alice y Bob estén conectados a la red minera, la mayoría de las transacciones de Alice llegarán directamente a la red minera y se propagarán rápidamente entre los nodos mineros. Una vez que los nodos mineros han difundido la transacción, se ignoran todos los intentos posteriores de los nodos completos de retransmitir la misma transacción.
Rechazo de transacciones duplicadas: el protocolo de Bitcoin garantiza que cuando el 100 % de los nodos mineros poseen una transacción, se descartan todas las transmisiones posteriores de la misma transacción desde otros nodos. Esto significa que en el 98,01 % de los casos en los que Alice y Bob están conectados directamente a los nodos mineros, el papel de los nodos completos en la propagación se vuelve completamente redundante. La transmisión inicial al nodo minero garantiza que la transacción ya esté disponible en toda la red y se ignoran todos los intentos de propagación por parte de los nodos completos. Integración matemática de probabilidades y latencia
Para cuantificar el tiempo total esperado para que una transacción se propague de Alice a Bob, podemos usar un promedio ponderado basado en las probabilidades de diferentes escenarios:
Tiempo de propagación esperado:
E(T) = P_directo * Tiempo de propagación_minería + P_indirecto * (Tiempo de propagación_nodos completos + Tiempo de propagación_minería)
Sustituyendo los valores:
E(T) = 0,9801 * 15 ms + 0,0001 * (280 ms + 15 ms)E(T) ≈ 14,7015 ms + 0,0001 * 295 msE(T) ≈ 14,7015 ms + 0,0295 ms = 14,731 ms
El tiempo esperado para que una transacción se propague de Alice a Bob es aproximadamente 14,73 ms. Este valor está dominado por el escenario en el que tanto Alice como Bob están conectados directamente a la red minera. La contribución de las rutas de nodos completos más lentas es casi insignificante debido a su baja probabilidad.
Conclusión: los nodos completos como un elemento superfluo en Bitcoin
Este análisis probabilístico detallado refuerza aún más la redundancia de los nodos completos en la red de Bitcoin:
– Alta probabilidad de conexión directa: con una probabilidad del 98,01 % de que tanto Alice como Bob estén conectados a la red minera, la mayoría de las transacciones evitan los cuellos de botella de latencia asociados con los nodos completos, confiando en cambio en la comunicación rápida entre los nodos mineros.
– Impacto mínimo de los nodos completos: la contribución de los nodos completos a la propagación de transacciones es estadísticamente insignificante. Incluso en los casos raros en los que están involucrados los nodos completos, los tiempos de propagación más lentos introducen demoras sin agregar valor.
– Rechazo sistemático de la propagación redundante: el diseño de la red de Bitcoin garantiza que una vez que los nodos mineros hayan recibido una transacción, cualquier intento posterior de los nodos completos de propagar la misma transacción se descarte como duplicado. Esto elimina la relevancia de los nodos completos para acelerar o ayudar al proceso de propagación.
Este riguroso análisis basado en la teoría de grafos demuestra que los nodos completos, aunque numerosos, no afectan significativamente la velocidad o la eficiencia de la propagación de transacciones de Bitcoin. La estructura eficiente y estrechamente conectada de los grupos de minería es lo que impulsa el rendimiento de la red de Bitcoin. Como resultado, los nodos completos solo sirven como observadores pasivos y su papel en la red más amplia es, en última instancia, superfluo. La verdadera funcionalidad y seguridad de la red se encuentran dentro de los nodos de minería activos e interconectados que controlan la validación de transacciones y la creación de bloques.

The Myth of Full Nodes
The Myth of Full Nodes
S. Tominaga AKA CSW
Oct 8, 2024
https://x.com/CsTominaga/status/1843529362341277972?t=sj_pGpCHtWYuzNw62pPvYA&s=19
-
Mining Nodes (Pools): A tightly interconnected network of 13-15 mining nodes, which are essentially mining pools. These form a complete graph, where every mining node is directly connected to every other.
-
Full Nodes: Between 5,000 and 10,000 full nodes with an average of 8 connections each, forming a sparse network with random connectivity patterns.
-
Graph Diameter: In a complete graph, the diameter (the longest shortest path between any two nodes) is 1. This means the distance between any two nodes is a single edge, making the propagation of information extremely efficient. The diameter D of K_{15} is:.
-
Propagation Time: Given the latency range of 5 ms to 15 ms, the worst-case time for a transaction to propagate across the entire network of mining nodes is:
-
There are approximately 5000 full nodes. Each full node has an average of 8 connections.
-
There are 13 to 15 mining nodes, which form a complete graph. In a complete graph, each mining node is directly connected to every other mining node.
-
It is given that there is a 99% chance that any given full node is connected to at least one mining node through one of its 8 connections.
-
With Full Nodes: Transactions from a full node take longer to reach mining nodes due to multiple hops in the sparse, random graph of full nodes.
-
Without Full Nodes: Every transaction would originate from or be relayed only through mining nodes, allowing for direct and immediate propagation between them. This reduces unnecessary delays caused by full nodes.
-
With Full Nodes: When a transaction originates from a full node, it must first hop through the sparse full node network to reach a mining node. This adds latency to the process, with an average of 1.041 hops for a transaction to reach the mining network.
-
Without Full Nodes: All transactions would originate from mining nodes or be propagated directly within the mining network. Since the mining nodes are fully connected, the transaction propagation time would be minimal—limited only by the direct communication speed between mining nodes, which is far faster than the full node network.
-
Efficiency With Full Nodes: Full nodes contribute to some network redundancy but slow down transaction propagation due to the random, less-connected nature of their graph structure. Their slower paths add unnecessary latency to the network.
-
Efficiency Without Full Nodes: The network would be more efficient without full nodes. Mining nodes, being tightly interconnected, handle transaction propagation directly and quickly. Removing full nodes would streamline the transaction flow, reducing latency and making the network faster overall.
-
Redundant Connectivity: Full nodes do not add useful paths for transactions. Instead, they introduce redundant routes that are slower and ultimately ignored once the mining nodes have completed their propagation.
-
Small-World Efficiency: The mining network’s small-world structure, with a diameter of 1, allows it to share information far more efficiently than the sprawling, high-latency connections of full nodes. This ensures that transactions are always processed through the fastest path—between mining nodes.
-
Lack of Influence on Network Control: From a decentralisation perspective, only those nodes involved in mining influence which transactions are included in blocks. Full nodes, by merely observing and broadcasting, do not participate in decision-making or block creation, making them irrelevant to the core concept of decentralisation.
-
Mining Nodes (Pools): A highly interconnected set of 13-15 mining nodes forming a complete graph K_n, where each node is directly connected to every other, facilitating rapid information sharing.
-
Full Nodes: A broader but sparser network of approximately 5,000 to 10,000 full nodes, each maintaining an average of 8 connections. These nodes typically connect randomly to other full nodes or directly to one or more mining nodes.
-
p_m = 0.99: A high probability that any given full node, such as Alice or Bob, is connected to at least one mining pool node, reflecting the reality that most full nodes connect to mining nodes for better access to network data.
-
p_f = 0.01: The remaining probability that a full node is connected only to other full nodes, without any direct connection to mining nodes.
-
Scenario 1: Direct Connection to a Mining Node: If Alice is directly connected to a mining node, the probability that her transaction reaches the mining network immediately is p_m. The same applies to Bob with probability p_m. The probability that both Alice and Bob are directly connected to the mining pool network is:
-
P_direct = p_m * p_m = 0.99 * 0.99 = 0.9801
-
This means there is a 98.01% chance that both Alice and Bob are connected to at least one mining node. In this case, Alice’s transaction, upon being sent, quickly reaches the mining node and is propagated through the entire mining network in a matter of milliseconds. Once the transaction is fully propagated among mining nodes, it will reach Bob via his connection to the mining network.The time taken for the transaction to reach all mining nodes is approximately:
-
Propagation Time_mining = 15 ms
-
Bob, being directly connected to the mining network, receives the transaction almost as soon as the mining nodes have propagated it, resulting in a very efficient transaction flow.
-
Scenario 2: Indirect Connection via Full Nodes: If Alice or Bob is part of the 1% of nodes not directly connected to any mining node (p_f), they must rely on their connections to other full nodes to propagate the transaction. The combined probability that neither Alice nor Bob is connected directly to a mining node is:
-
P_indirect = p_f * p_f = 0.01 * 0.01 = 0.0001
-
This means there is a 0.01% chance that both Alice and Bob lack a direct connection to a mining node. In this rare scenario, the transaction propagation would have to occur through the slower, multi-hop paths of the full node network: Full Node Latency Impact: A transaction from Alice would travel through approximately 4 hops in the random full node network before potentially reaching a mining node, with each hop taking 60 ms to 80 ms. The total propagation time before reaching a mining node would be:Propagation Time_full nodes = 4 * 70 ms = 280 ms Once the transaction reaches a mining node, it is then quickly propagated through the mining network. However, due to the initial delay through the full node network, the transaction reaches Bob far later than it would have if Alice had a direct connection to the mining network.
-
Duplicate Transaction Rejection: The Bitcoin protocol ensures that when 100% of mining nodes possess a transaction, any further transmissions of the same transaction from other nodes are discarded. This means that in 98.01% of cases where Alice and Bob are both directly connected to mining nodes, the role of full nodes in propagation is rendered completely redundant. The initial transmission to the mining node ensures that the transaction is already available throughout the network, and any propagation attempts by full nodes are ignored.
-
Expected Propagation Time:
-
Substituting the values:
-
The expected time for a transaction to propagate from Alice to Bob is approximately 14.73 ms. This value is dominated by the scenario in which both Alice and Bob are directly connected to the mining network. The contribution of the slower full node paths is almost negligible due to their low probability.
-
High Probability of Direct Connection: With a 98.01% chance that both Alice and Bob are connected to the mining network, most transactions avoid the latency bottlenecks associated with full nodes, relying instead on the rapid communication between mining nodes.
-
Minimal Impact of Full Nodes: The contribution of full nodes to transaction propagation is statistically insignificant. Even in the rare cases where full nodes are involved, the slower propagation times introduce delays without adding value.
-
Systematic Rejection of Redundant Propagation: The Bitcoin network’s design ensures that once mining nodes have received a transaction, any further attempts by full nodes to propagate the same transaction are dismissed as duplicates. This eliminates the relevance of full nodes in speeding up or aiding the propagation process.





Dejar un comentario
¿Quieres unirte a la conversación?Siéntete libre de contribuir!